1. 概览
本文由大师Chandy和Lamport所著,也是一篇老物了,1985年了。但是文章非常经典,它是Flink等系统实现快照的基础,所以拿来阅读一下。
个人感觉,原理还是不难的,但是其背后的证明非常难懂/绕,我搞的也不是很透彻。
废话少说,现在就开始看论文的内容。
1.1. 术语定义
- $D$:某个分布式系统
- $S$:分布式系统的全局状态
- $y$:一个谓词
- $y(S)$:给定一个分布式系统的全局状态,返回
true/false
- $y(S)$:给定一个分布式系统的全局状态,返回
- 稳定属性(stable property):
- 对于某个全局状态$S$,若对所有从$S$开始可达的全局状态$S’$,都有$y(S) \rightarrow y(S’)$,则$y$就是稳定属性
- 也即:若$y$是一个稳定属性,且当某个点$y$为
true,之后所有可达的点$y$也为true - 稳定属性的例子:
- 计算已停止
- 系统已死锁
- 环上所有的token都消失了
1.2. 本文焦点
本文提出一个算法,用于检测一个分布式系统的稳定属性。
而确定稳定属性,则需要全局状态/全局快照,因此这里也会描述全局状态/快照的收集算法。
2. 系统建模
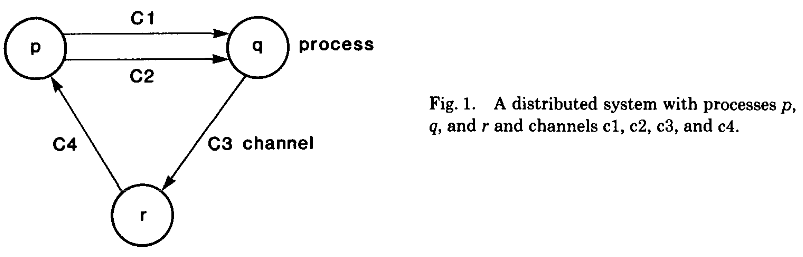
分布式系统由2部分组成,可描述为一个有向图:
- 一组进程(process,以顶点描述)
- 一组进程通信通道(channel,以边描述)
2.1. 通道、进程与事件
通道、进程和事件需要一些的定义:
- 通道$c$:
- 单工(所以是有向图)
- 拥有无限的缓冲区、不会出错、消息传输有序、不重复
- 延迟是任意但有限的
- 通道的状态定义为:已发送的消息序列(不含接收的消息)
- 进程$p$:由三个东西组成
- 一组状态集
- 初始状态
- 一组事件
- 事件$e$:一个原子操作,可能改变进程$p$和至多1个通道$c$的状态
- 通道的状态可通过发送或者接收消息改变
- 事件可通过$\langle p, s, s’, M, c \rangle$描述,分别为进程、进程前后状态、发送/接收的消息、消息所在的通道(后两项可为空,表示事件没改变通道状态)
2.2. 全局状态
全局状态的定义也就很简单了,就是系统所有进程和通道的状态。
全局初始状态:
- 进程处于一个初始状态
- 通道状态为空序列
全局状态会因为事件而改变,而事件$e = \langle p, s, s’, M, c \rangle$能发生在全局状态$S$的条件为:
- 进程$p$在$S$的状态为$s$
- 若通道$c$指向$p$,通道$c$在$S$的状态满足:$head(c) = M$
改变后的状态记为$S’$,这里定义$next(S, e)$函数,满足: \(S’ = next(S, e)\) $S’$满足下面的属性:
- 进程$p$在$S’$的状态为$s’$
- 通道$c$在$S’$的状态满足:
- 若$c$指向$p$:$M$从$c$的头部删除
- 若$c$从$p$出发:$tail(c) = M$
2.3. 一个例子:Single-token Conservation System
有2个进程$p$,$q$,它们互相有一个通道$c$和$c’$。两个进程相互传一个token。
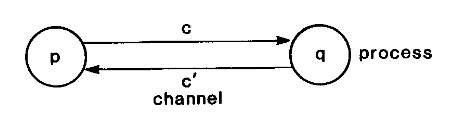
我们定义:
- 进程有2个状态:$s_0$代表进程没有token,$s_1$代表进程有token
- 初始状态:
- 进程$p$状态为$s_1$,进程$q$状态为$q$状态为$s_0$
- 两通道$c$和$c’$状态为$\emptyset$
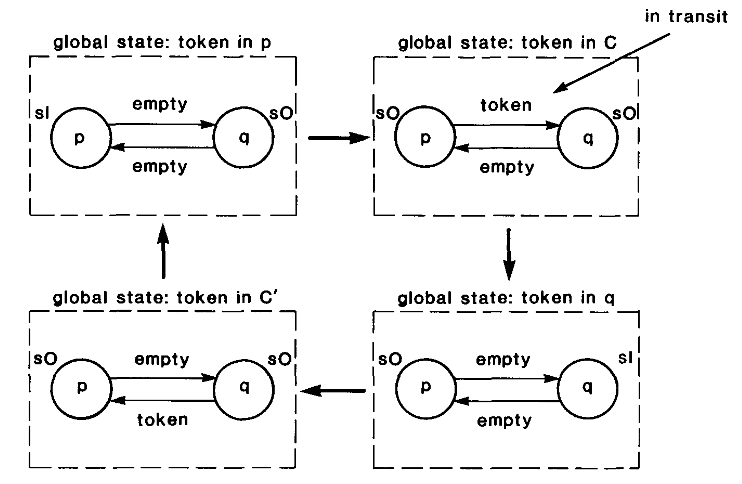
那么状态转移图就如下所示,涉及到4个事件分别为:
- $\langle p, s_1, s_0, c, token \rangle$:$p$发送token
- $\langle q, s_0, s_1, c, token \rangle$:$q$收到token
- $\langle q, s_1, s_0, c’, token \rangle$:$q$发送token
- $\langle p, s_0, s_1, c’, token \rangle$:$p$收到token
3. 全局状态/快照收集算法
3.1. Motivation
这里定义一个最简单的分布式系统:2.3.的例子
假定:
- $n$:$p$状态被记录前,$p$向$c$发送的消息个数
- $n’$:$c$状态被记录前,$p$向$c$发送的消息个数
- $m$:$q$状态被记录前,$q$收到从$c$中的消息个数
- $m$:$c$状态被记录前,$q$收到从$c$中的消息个数
为了保证一致性,可以得到: \(\begin{eqnarray*} n = n' \tag{1} \\ m = m' \tag{2} \\ n' \ge m' \tag{3} \\ n \ge m \tag{4} \end{eqnarray*}\) 由于$c$的状态是$p$发送的消息序列,序列必须是在发送者$p$记录其状态之前的。但是作为$p$,实际上你是不知道$c$到底有多少东西(因为有些东西已经发到网络了,但有些东西还在缓冲,且$c$是单工的,不能通过ACK进行计数)。
所以这里引入一个新的消息类型marker。它类似于一个栅栏,将其插入到通道队列中,但它不参与任何的状态计算。当接收者$q$收到marker后,根据这个为界,记录$c$中序列。
3.2. Global-State-Detection Algorithm/Chandy-Lamport Algorithm
算法满足下面2个规则:
- Marker-Sending Rule:对于发送者$p$,在记录自己状态后,且在$p$发送后面的消息前,给所有的通道$c$(这里$c$从$p$开始)发送一个marker
- Marker-Receiving Rule:对于接收者$q$
- 若$q$没有记录状态,则先记录自己的状态,并记通道$c$的状态为$\emptyset$
- 若$q$记录了状态,则收集从自己记录状态后,到marker之间的消息序列,该序列就是通道$c$的状态
所以,基于上面2个规则,算法的总结如下:
a) 发起Snapshot
选取一个或多个进程$p$:
- 记录自己进程的状态
- 向所有通道$c_{pq}$发送marker(注意通道是单工的)
b) 传播Snapshot
对于接收进程$q$:
- 假如$q$没有记录自己的状态
- 记录自己进程的状态
- 记通道$c_{pq}$的状态为空
- 向所有通道$c_{qr}$发送marker
- 记录所有从其它通道$c_{oq}$($o \ne p$)接收到的消息序列(从记录自己状态之后开始),这些通道的状态为这些序列
- 假如$q$已经记录自己的状态
- 记录所有从其它通道$c_{oq}$($o$可以取$p$)接收到的消息序列(从记录自己状态之后开始),这些通道的状态为这些序列
c) 终止Snapshot
由于假设通道不出错、有限延时、不重复、不乱序等等,每个进程$p$最终都会记录自己以及所有输入通道$c_{op}$的状态。
而为了达到上面的要求,让算法终止,每个进程必须保证:
- 所有的输入通道中没有marker,即从每个通道中都收到了marker
- 记录状态需要在有限时间内完成
4. 全局状态/快照的特性
这里令:
- $seq = (e_i, 0 \le i)$:事件列表
- $S_i$:执行事件$e_i$前的全局状态
- 全局状态步获算法从$\iota$开始,到$\phi$结束,即
- 从$e_{\iota-1}$后,$e_{\iota}$前开始捕获(开始时为$S_\iota$)
- 到$e_{\phi-1}$后,$e_{\phi}$前完成捕获(结束时为$S_\phi$)
- $0 \le \iota \le \phi \le i$
a) 可达性
在非确定性计算中,很有可能实现执行的顺序不按照原本的$seq$执行。
那么很可能会捕获到这样的状态$S^{*}$,它和$S_k (\iota \le k \le \phi)$(这里$S_k$对应的是$seq$原本的执行顺序)都不相同。
这个$S^{*}$满足:
- 从$S_{\iota}$开始,$S^{*}$可达
- 从$S^{*}$开始,$S_\phi$可达
b) 事件序列
此外,根据上面的情形,存在一个事件序列$seq’$,满足:
- $seq’$是$seq$的一个排列,$S_{\iota}, S^{*}, S_{\phi}$三个状态都在这个序列中出现
- $S_{\iota} = S^{}$,或者$S_{\iota}$先于$S^{}$
- $S_{\phi} = S^{}$,或者$S_{\phi}$后于$S^{}$
c) 上述结论的总结
实际上,a)和b)可描述为一个定理,如下所述:
有原事件序列$seq = (e, 0 \le i)$,存在一个事件序列$seq’ = (e’, 0 \le i)$,满足:
- $\forall i, i \lt \iota \lor i \ge \phi$,有$e_{i}^{‘} = e_{i}$
- 子序列$(e’, \iota \le i \lt \phi)$是子序列$(e, \iota \le i \lt \phi)$的一个排列
- $\forall i, i \lt \iota \lor i \ge \phi$,有$S_{i}^{‘} = S_{i}$
- $\exists k, \iota \le k \le \phi$,有$S^* = S_{k}^{‘}$
d) 定理证明
首先定义2个概念:
- pre-recording event:对于进程$p$的事件$e_i$,$e_i$发生在$p$记录状态之前
- post-recording event:对于进程$p$的事件$e_i$,$e_i$不是pre-recording event
易得知:对于$\forall i \lt \iota$,$e_i$是pre-recording event;对于$\forall i \ge \phi$,$e_i$是post-recording event。
然而对于一个真实场景,$seq$中的$e_{j-1}$可能会发生在$e_{j}$之前,这里$\iota \lt j \lt \phi$(发生在不同进程上),导致post-recording event发生在pre-ordering event之前。
所以,这里生成另一个事件序列$seq’$,它是$seq$的一个排列,且满足pre-recording event一定发生在post-recording event之前(如上面的例子,可能有$ e^{‘}{j-1} = e{j}, e^{‘}{j} = e{j-1} $)。下面会证明:$S^{*}$就是在所有pre-recording event之后,post-ordering event之前的全局状态。
首先证明一个结论:假如一个post-recording event $e_{j-1}$发生在pre-recording event $e_{j}$前,那么将它们交换依旧有效(依旧是一个computation),且交换过的序列执行得到的状态和原来的一样。
-
在这种情况下,$e_{j-1}$和$e_j$肯定不在一个进程上(若在一个进程,必满足FIFO顺序)。那么交换它们是无所谓的。
-
在上面的情况下,假定进程$p$执行$e_{j-1}$,进程$q$执行$e_j$,那么不可能有消息在$e_{j-1}$发出,在$e_j$接收。
利用反证法。
第一,当$e_{j-1}$发生,通过$c$向$q$发送一条消息,那么在发送消息前,肯定有marker被发送过去,因为$e_{j-1}$是post-recording event;
第二,当$e_j$发生,$q$从$c$获取这条数据,那么在这之前一定收到了marker,这样$e_j$也就成为post-recording event,矛盾。
-
基于上面,可以得出$e_j$发生时,若$q$从$c$中读到消息$M$,该消息一定发生在$e_{j-1}$之前,$e_j$也能出现在$S_{j-1}$中。而且$e_j$发生时,$p$是不会改变状态的(同理$e_{j-1}$发生时,$q$不会改变状态),所以$e_{j-1}$和$e_{j}$可以调换顺序,且最后得到的全局状态和原来是一样的。
即$seq’$作为$seq$的一个排列,它只将上述的$e_j$和$e_{j-1}$交换,令$\bar{S_{i}}$为$seq’$下第$i$个事件前的全局状态,有: \(\bar{S_{i}} = S_{i} (\forall i, i \ne j)\) 那么根据上面的结论,我们只要不停的交换pre-recording event $e_{j}$和post-recording event $e_{j-1}$,我们就可以得到这样一个序列$seq’$,满足:
- 它是$seq$的一个排列
- $seq’$中,pre-ordering events必在post-recording events之前
- $\forall i, i \lt \iota \lor i \ge \phi$,有$ e^{‘}{i} = e{i} $
- $\forall i, i \lt \iota \lor i \ge \phi$,有$ S^{‘}{i} = S{i} $
至此,我们证明了c)中的前3条性质。
现证明最后一条性质:$\exists k, \iota \le k \le \phi$,有$S^* = S_{k}^{‘}$。证明它需要证明:
- $S^*$中,每个进程$p$的状态,和它们处理完序列中pre-recording event的状态一样;
- $S^*$中,每个通道$c$的状态为:所有pre-recording event发往$c$的序列减去所有pre-recording event从$c$中收到的序列。
第1点是显而易见的(trivial),所以只需证明第2点:
- 令$c: p \rightarrow q$
- 状态$S^*$中的$c$的状态是从$q$记录自己状态之后,收到marker之前的消息序列,这个序列等于$p$发送marker之前,pre-recording events向$c$发的。第2点得证。
至此,第4条性质得证。于c)中的定理证毕。
其实这段证明非常绕,我也没理解透彻。个人感觉关键的2点:
- $e_{j}$和$e_{j-1}$事件没有因果关系,所以交换顺序不影响结果;
- 得到的全局状态$S^*$,是指处理完pre-recording event后的系统状态。这里marker作为“栅栏”的重要性。
5. 稳定属性检测
最后,回到第1节的稳定属性检测。有了第3节和第4节的基础,稳定属性的检测就变得比较简单了。
稳定属性检测的算法的定义如下:
-
输入:一个稳定属性$y$
-
输出:一个
bool值$definite$,它满足$(y(S_\iota) \rightarrow definite) \land (definite \rightarrow y(S_\phi))$,其中$S_\iota, S_\phi$分别代表算法初始和结束的全局状态满足条件可改写成$(\neg y(S_\iota) \lor definite) \land (\neg definite \lor y(S_\phi))$
-
若返回
true:表示稳定属性在算法终止时满足谓词,但不代表稳定属性在算法开始时满足若$definite$为真,$y(S_\phi)$必须为真,但是$y(S_\iota)$没法判断。即它给了算法结束时的状态。
-
若返回
false:表示稳定属性在算法开始时就不能满足谓词,但不代表稳定属性在算法终止时不满足若$definite$为假,$y(S_\iota)$必须为假,但是$y(S_\phi)$没法判断。即它给了算法开始时的状态。
-
而实现它的方法很简单:
1
2
3
4
5
def stability_detection(y):
S_star = record_global_state() # With S_iota and S_phi
definite = y(S_star)
return definite
其正确性证明很简单:
- 第4节涉及的定理:
- 从$S_{\iota}$开始,$S^{*}$可达
- 从$S^{*}$开始,$S_\phi$可达
- 稳定属性定义:对所有从$S$开始可达的全局状态$S’$,都有$y(S) \rightarrow y(S’)$