Distributed System Paper

论文阅读-Lightweight Asynchronous Snapshots for Distributed Dataflows

Posted by keys961 on February 18, 2020

1. 概览

本文介绍了一个轻量、异步的快照算法，Flink就是基于这个算法，实现了一致性快照和exactly-once的特性的，并保证执行快照时计算的低延迟、高吞吐。

该算法主要概览：

  • 轻量、异步
  • 快照只包含算子的状态，适用的数据流拓扑结构为无环图，也适用于有环图（利用下游备份）

本算法的一个关键基础是 Chandy & Lamport 的快照算法，其关键的思想就是插入barrier marker。详细可参考：

2. Apache Flink

Apache Flink是一个可用于批和流处理的计算系统。

Flink中，流/批处理计算由一系列相连的有状态任务组成的，因此Flink会将任务编译成一个有向图：

  • 顶点代表一个有状态任务，根据输入维护自己的状态，并向下游输出数据流
  • 数据流在顶点之间的边上传输

2.1. 流处理模型

Flink API中，数据流被抽象为DataStream：

  • 支持很多算子（如map, filter, reduce）以生成新的DataStream
  • 算子支持并行化，这基于DataStream分区

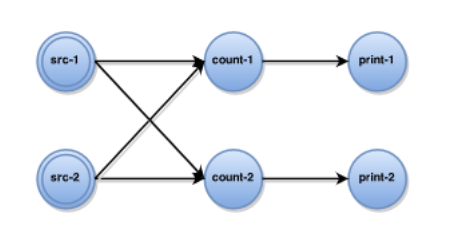
一个增量计算单词个数的例子

代码：

1
2
3
4
5
6
7
8

val env :StreamExecutionEnvironment = ... 
env.setParallelism(2) // 并行度2

val wordStream = env.readTextFile(path)
val countStream = wordStream
	.groupBy(_) // (group是一个stream -> table操作)
	.count
countStream.print

拓扑结构：

topology

2.2. 分布式数据流执行

上面的例子已经展示了一个流处理计算会被编译成一个有向图$G = (T, E)$：

  • $T$：表示计算的任务，对于某个顶点$t \in T$，它是一个算子的独立执行实例，并包含

    • $I_{t}, O_{t} \subseteq E$：输入和输出
    • $s_{t}$：状态
    • $f_{t}$：用户自定义函数

    顶点消费输入的数据，更新算子状态，并根据自定义函数生成并输出数据。

  • $E$：表示任务之间的数据通道

  • $M$：任务间传输的所有记录集合。

3. Asynchronous Barrier Snapshotting

3.1. 问题定义

全局快照：$G^{} = (T^{}, E^{*})$

  • $T^{}$：记录所有$t \in T$的状态$s_{t}^{}$
  • $E^{}$：记录了所有通道$e \in E$中所有在途的数据$e^{}$

算法满足下面2个特性

  • 可终止：若所有进程存活，算法最终会在有限时间内完成
  • 可行性：这包含很多含义，最主要的，快照保持了因果顺序

3.2. 无环图ABS

基本思想：周期性在source端插入barrier marker。

  • barrier marker会从source传到sink
  • 通过传播，快照被一步一步的构建出来

算法假设：

  • 网络基本可靠：保证FIFO顺序，可阻塞也可非阻塞（阻塞时数据在缓冲，不被发送）

  • 任务可操作通道：操作有block, unblock, send, broadcast
  • 在source端，输入被放入Nil的输入通道

那么算法的伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

struct Task {
    input_channels, // 输入通道集合
    output_channels, // 输出通道集合
    state, // 状态
    udf, // 用户自定义函数
    blocked_input_channels, // 阻塞的输入通道集合
    // ...
}

// 初始化
fn init(input_channels, output_channels, fun, init_state) {
    self.input_channels = input_channels;
    self.output_channels = output_channels;
    self.udf = fun;
    self.state = init_state;
    self.blocked_input_channels = Set::new();
}

// 接收数据后的回调
fn event_recv(input_channel, msg) {
    // 计算新状态并得到输出数据
    (new_state, output_records) = self.udf(msg, self.state);
    // 更新状态
    self.state = new_state;
    // 输出到下游
    for (out_record, out_channel) in output_records {
        send(out_channel, out_record);
    }
}

// 接收barrier marker的回调
fn event_recv_barrier(input_channel, barrier) {
    if input_channel != Nil {
        // 将输入通道阻塞
        self.blocked_input_channels.add(input_channel);
        block(input_channel);
    }
    if self.blocked_input_channels == self.input_channels {
        // 若输入通道全部阻塞
        // 清空集合
        self.blocked_input_channels.clear();
        // 广播barrier到所有下游(所有输出通道)
        broadcast(self.output_channels, barrier);
        // 做当前节点的快照
        snapshot(self.state);
        // 解除阻塞输入通道
        for input in self.input_channels {
            unblock(input);
        }
    }
}

可终止：这是基于无环图的算法，由于无环图必定有一个拓扑排序，当排序的最后一个顶点完成快照后，快照算法必定会结束。

可行性：而网络通道的FIFO特性和可阻塞性，保证了快照的可行性，维护了因果顺序。

该算法和 Chandy & Lamport 快照算法非常像（就是传播Snapshot的第一个分支），很容易得知，最后得到能得到快照$G^{} = (T^{}, E^{})$，且$E^{} = \emptyset$。

3.3. 有环图ABS

对于有环图，3.2.的算法就会有死锁的问题，且不能捕捉通道中的数据，有违“可行性”。

这里，有环图ABS算法在无环图基础上：

  • 利用DFS，找到有向图$G$的back-edge集合$L$（这样$G = (T, E-L)$就是一个无向图了）
  • 进行下游数据的备份，备份的下游数据是在创建快照时，从back-edge中收到的数据
    • 对于一个任务$t$，它有一个输入back-edge集合$L_{t}$。$L_{t}$会创建备份日志
    • 日志记录从$L_{t}$收到的数据，范围：
      • 开始：任务$t$传播barrier marker到下游开始
      • 结束：收到$L_{t}$的barrier marker

所以整个算法的伪代码如下，解释可看下面的注释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

struct Task {
    input_channels, // 输入通道(包含back edge)集合
    output_channels, // 输出通道集合
    loop_input_channels, // back edge输入通道集合
    marked_input_channels, // 标记(收到barrier marker)的输入通道集合
    state, // 状态
    state_copy, // 某个时刻状态的拷贝，快照存储的数据使用了该字段
    udf, // 用户自定义函数
    logging, // 是否在记日志
    backup_log, // 日志列表
    // ...
}

// 初始化
fn init(input_channels, backedge_channels, output_channels,
        fun, init_state) {
    self.state = init_state;
    self.state_copy = Nil;
    self.input_channels = input_channels; // 包含了back edge
    self.output_channels = output_channels;
    self.loop_input_channels = backedge_channels; // back edge input channel
    self.marked_input_channels = Set::new();
    self.udf = udf;
    self.logging = false;
    self.backup_log = vec![];
}

// 接收数据后的回调
fn event_recv(input_channel, msg) {
    if self.logging && self.loop_input_channels.contains(input_channel) {
        // 若打开了logging, 且输入的通道是back edge, 则要将数据添加到日志里
        self.backup_log.append(msg);
    }
    // 计算新状态并得到输出数据
    (new_state, output_records) = self.udf(msg, self.state);
    // 更新状态
    self.state = new_state;
    // 输出到下游
    for (out_record, out_channel) in output_records {
        send(out_channel, out_record);
    }
}

// 接收barrier marker的回调
fn event_recv_barrier(input_channel, barrier) {
    // 收到barrier, 首先标记对应的输入通道
    self.marked_input_channels.add(input_channel);
    // 作差集, 获取非back edge的输入通道
    let regular_input_channels = self.input_channels - self.loop_input_channels;
    if input_channel != Nil && !self.loop_input_channels.contains(input_channel) {
        // 若输入通道不是back edge, 将其阻塞
        block(input_channel);
    }
    if !self.logging && self.marked_input_channels == regular_input_channels {
        // 当所有的非back edge输入通道都被标记了, 即都被阻塞了
        // 则开始记录back edge驶入通道的日志
        // 并广播barrier到下游, 将取消之前通道的阻塞
        // 注意，这里用‘==’是因为算法保证back edge永远是最后加入/标记的
        self.logging = true;
        // 注意这里保存了当前的状态拷贝, 它是本轮snapshot需要记录的状态
        self.state_copy = state;
        broadcast(self.output_channels, barrier);
        for input_channel in self.input_channels {
            unblock(input_channel);
        }
    }
    if self.marked_input_channels == self.input_channels {
        // 当所有的输入通道被标记, 且back edge也被标记
        // 那么记录状态: (state_copy, backup_log)
        // 前者是上面代码记录的拷贝, 代表日志记录前的状态
        // 后者是self.logging开启后, 通过event_recv函数记录的日志
        // 它可用来代表back edge上传输的消息快照, 因为state_copy不含back edge的数据影响
        snapshot(self.state_copy, self.backup_log);
        // 清空状态,关闭日志记录
        self.marked_input_channels.clear();
        self.state_copy = Nil;
        self.backup_log.clear();
        self.logging = false; 
    }
}

其实有环图ABS的算法，也是衍生自 Chandy & Lamport 快照算法（就是再加上Snapshot传播的第二个分支），本质上几乎是一样的。易知，最后得到能得到快照$G^{} = (T^{}, E^{})$，且$E^{} = L^{*}$。

可终止：每个任务$t$都能最终收到所有输入通道（包含back-edge）的barrier mark，且通过广播barrier mark将其传播到下游，直到所有任务都收到。死锁也避免了，这通过不阻塞back edge输入通道完成（这样就不会造成一个阻塞环了）；

可行性：依旧是网络通道的FIFO特性来保证：

  • 快照中的任务状态，即state_copy，不包含收到barrier marker后的状态
  • 快照中的下游日志是完整的，它的范围从$E-L$收到barrier marker开始，到收到$L$的barrier marker结束，这通过FIFO网络通信保证

4. 错误恢复

错误恢复有很多方法，最简单的是：

  • 每个任务$t$读取快照$G^{}_{t} = (T^{}{t}, E^{*}{t})$
  • 设置初始状态为$T^{}_{t}$，并重新执行日志$E^{}_{t}$，以恢复状态
  • 重新开始接收上游数据

此外，子图恢复也是可行的：只要恢复失效任务$t$及其上游（到source）即可。如下图所示：

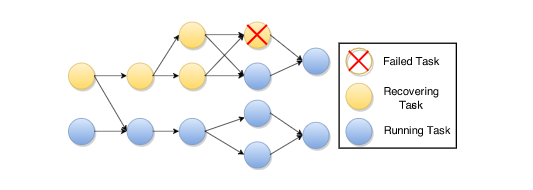
partial_graph_recovery

为了达到exactly-once语义，下游需要去重（以避免重计算）。去重可以通过标记序列号实现。

5. 总结

实际上，这篇论文提供的ABS算法实现，本质上和 Chandy & Lamport 快照算法是一样的。它其实只做了2个优化：

  • 异步执行
  • 降低要保存的快照数据量
    • 无环图可不存通道上的数据
    • 有环图只需存back-edge通道的数据
CATALOG
    FEATURED TAGS
    Algorithm Java Network Distributed System Stream Processing Operating System Paper Linux Redis etcd Kubernetes C++