1. 概述

本节将算法概述性地描述一下。

插入很直接：

• 先创建新节点，设置新节点的next指针
• CAS设置前置节点的next指针，即compare_and_swap(&prev->next, prev_next, &new_node)

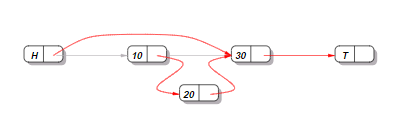
上述操作，对于多线程插入是没问题的，但是一旦涉及删除操作，就会出现问题，例如下图中同时删除10和插入20，连接前面节点的CAS都会成功，但是数据结构会被破坏：

本文的解决方法是：使用2步CAS

• 第一步：CAS给待删除的节点的next指针设置标记mark，即逻辑删除
  • 该标记可以作用于next指针的某一位，例如目前64位指针只利用了48位，有例如内存对齐导致的后面几位也没使用
  • 若成功设置mark，插入时CAS连接前一个节点时就会失败，然后重试
• 第二步：CAS连接删除操作所需的前一节点的next指针，释放内存，即物理删除
  • 此时，重试的插入就能成功，且不会破坏数据结构

2. 算法实现

假定我们用这个链表定义一个有序的集合，那么实现如下。

Github找到某个人的实现：https://github.com/alwaysR9/lock_free_ds/blob/master/list/lock_free_list/lock_free_list.cpp

2.1. 数据结构定义

首先定义数据结构：

typedef struct List {
    Node *head;
    Node *tail;
} List;

typedef struct Node {
    void *value;
    volatile Node *next;
} Node
    
List *newList() {
    List *list = (List *)malloc(sizeof(List));
    list->head = newNode(NULL);
    list->tail = newNode(NULL);
    list->head->next = list->tail;
}

Node *newNode(void *value) {
    Node *node = (Node *)malloc(sizeof(Node));
    node->value = value;
    node->next = NULL;
    return node;
}

int compare(void *a, void *b) {
    // ... Self defined ...
    // 0: equal, -1: a < b, 1: a > b
}

2.2. 插入

由第1节所述，插入是很直接的，不需要处理和转换mark标记，所以代码就是一个CAS循环：

int insert(List *list, void *value) {
    Node *node = newNode(value);
    Node *prev, *after;
    do {
        search(list, value, &prev, &after); // 查找节点
        if(after != list->tail && compare(after->value, value) == 0) {
            free(node);
            return 0; // 重复, 直接返回
        }
        node->next = after;
        if(compare_and_swap(&(prev.next), after, node)) {
            // CAS设置前置节点的next指针, CAS本身会检测mark, 因为mark是在next指针内
            return 1;
        }
    } while(1);
}

2.3. 删除

删除分为2步：逻辑删除和物理删除。代码如下所示：

int delete(List *list, void *value) {
    Node *prev, *cur, *after;
    do {
        search(list, value, &prev, &cur);
        if(cur == list->tail || compare(value, cur->value)) {
            // 没找到, 退出
            return 0;
        }
        after = cur->next;
        // 1. 执行逻辑删除, CAS设置mark
        if(!is_marked_ref(&(cur->next))) {
            if(compare_and_swap(&(cur->next), after, marked_ref(after))) {
                break;
            }
        }
    } while(1);
    // 2. 执行物理删除: CAS连接前后节点
    if(!compare_and_swap(&(prev->next), cur, after)) {
        // CAS失败, 执行一次search, search会保证:
        // a. cur, after相邻且不会被标记
        // b. 中间的marked节点会被删除
        // 由于CAS失败,说明prev->next != cur
        // 通过search遍历,有顺序保证,可以保证已标记的cur会被删除
        // 后面会说明
        search(list, value, &prev, &cur);
    } else {
        free(cur);
    }
    return 1;
}

而标记地址，可以利用一些架构的特性，例如64位x86架构，可挑选前16位的某一位（因为只使用48位），也可以使用后4位的某一位（因为对齐），例如下面的实现：

Node *marked_ref(Node *origin) {
    return (Node*) ((unsigned long)origin | (unsigned long)0x1);
}

Node *unmarked_ref(Node *marked) {
    return (Node*) ((unsigned long)marked & ~(unsigned long)0x1);
}

int is_mark_ref(Node *ref) {
    return ((unsigned long)marked & (unsigned long)0x1);
}

2.4. 查找

查找就比较简单了，利用search函数，直接一遍遍历即可：

Node *find(List *list, void *value) {
    Node *prev, *cur;
    search(list, value, &prev, &cur);
    if(cur == list->tail || compare(cur->value, value)) {
        return NULL;
    }
    return cur;
}

而search函数，在之前的几个操作中都有使用，它除了查找之外，还有下面的特性：

• 返回两个指针prev和cur，它们相邻且都没被标记
• 返回的prev和cur在调用search前，可能不是相邻（即中间有被标记的节点），中间标记的节点在search后会被移除
• 列表是有序的，保证prev恰好小于给定的value

void search(List *list, void *value, Node **prev, Node **cur) {
    Node *prev_next;
search_again:
    do {
        Node *t = list->head;
        Node *t_next = list->head->next;
        // 1. 找prev和cur
        do {
            if(!is_marked_ref(t_next)) {
                (*prev) = t; // 这里保证prev肯定没被标记
                prev_next = t_next;
            }
            t = unmarked_ref(t_next);
            if(t == list->tail) {
                break;
            }
            t_next = t->next;
        } while(is_marked_ref(t_next) || compare(t->value, value) < 0);
        *cur = t;
        // 2. 检查相邻
        if(prev_next == *cur) {
            if(*cur != list->tail && is_marked_ref((*cur)->next)) {
                goto search_again; // 相邻但后面的节点被标记，则重新搜索
            } else {
                return; // 就是正确结果
            }
        }
        // 3. 删除被标记的节点
        if(compare_and_swap(&((*prev)->next), prev_next, *cur) {
            // cur和prev不是相邻,说明prev_next被标记,则需要删除
            free(prev_next);
            if(*cur != list->tail && is_marked_ref((*cur)->next)) {
                // 若cur被标记 => 还是需要重新搜索一次,并将其移除
                // 一轮只移除一个marked节点,直到没有为止
                // 但不会移除后面的marked节点
                goto search_again;
            } else {
                return;
            }
        }
    } while(1);
}

3. 正确性证明

这部分略过，作者证明了算法的正确性（通过search保证）、线性一致以及非阻塞性，并利用模型检查和实际测试表明算法的正确性。

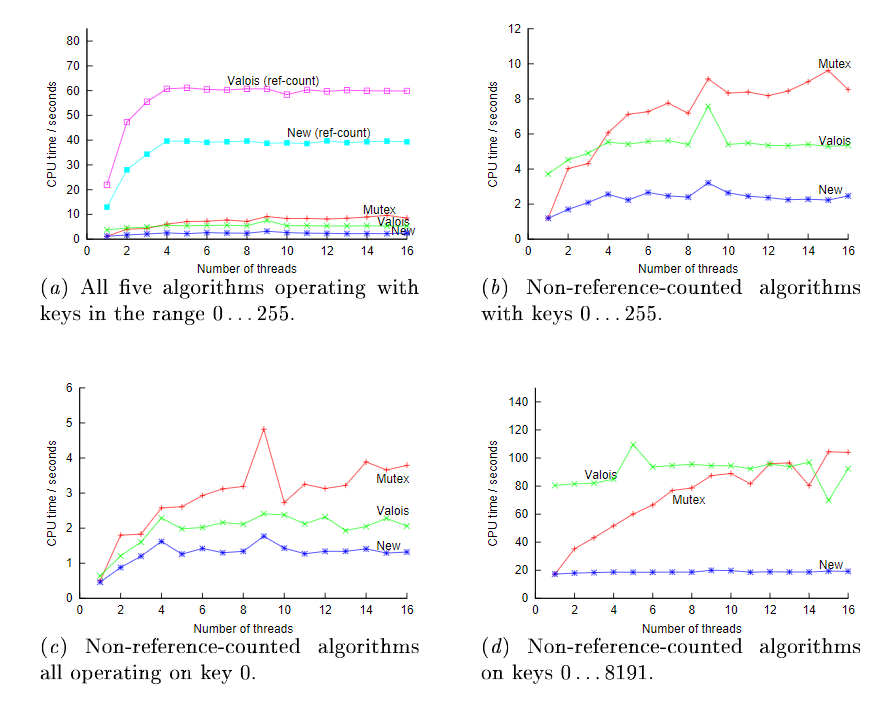
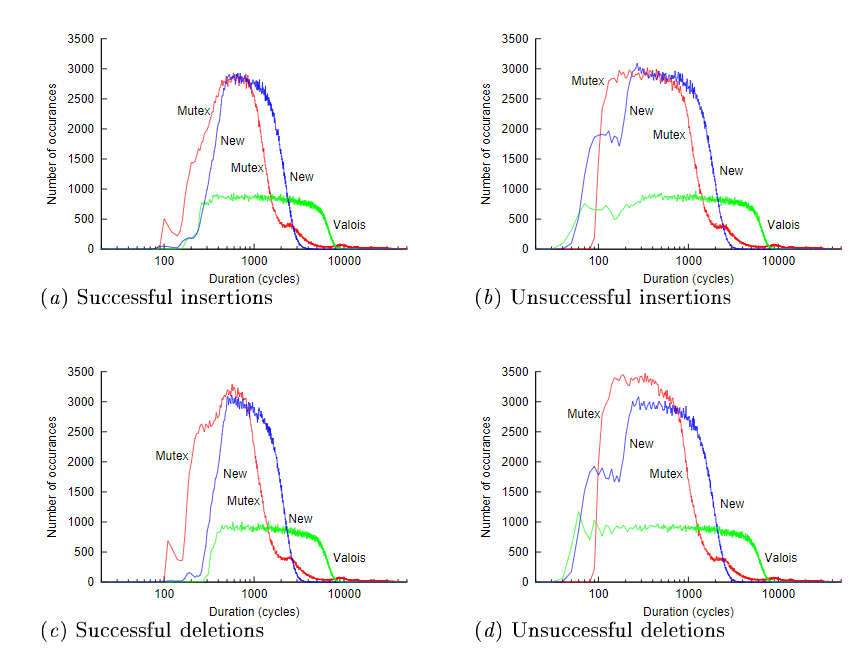
4. 测试结果

这里就放两张图，详细的还是看论文好了。（这里Valois就是辅助节点法的实现）

• Previous
  论文阅读-Lock-Free Linked List Using Compare-and-Swap
• Next
  Leetcode: Super Egg Drop