1. 背景

• 数据以table形式存储

  • 多数read-only

  • 多数以时间partition（以天）

• 多个相关table组织成project

• 每个计算负载称为job

  • 它需要读取table

  • job间有依赖（dependency），依赖可能导致cross-DC的数据传输

本文需要控制cross-DC的访问，降低其流量，提高效率。

2. 负载分析

2.1. Project, Table & Job

• Project：绝大部分很小，但很小一部分特别很大（符合power-law distribution）

  对应Project Placement，只需处理优化（放置）小部分Project，就能得到很好的效果

• Job：

  • Input partition比Output partition多

  • Input数据量比Output数据量多（即读比写多）

• Table：一个partition的大小很小，占整个table很小一部分

2.2. 依赖分析

• cross project的访问占6成，cross DC访问占3成，非常大

• cross DC的访问流量主要由下面的贡献

  • hot table

  • large project

2.3. Table访问模式

• 基本每天append新的partition，大小都差不多

• job访问table的量，每天都差不多

• 最近的partition访问量多，往后指数级别下降

2.4. 潜在获益点

• 一些table会被很多job频繁的cross-DC访问，若将其复制到job所在到DC，可以节省流量

  对应Table Replication

• 对job调度优化，若将其调度到table所在到DC，可以节省流量

  对应Job Outsourcing

2.5. 资源利用情况

不同DC的资源利用不可预测，不同时间可能出现不同的瓶颈。

3. 论文中的优化方法

3.1. Project Placement (Offline)

将新Project放到一个DC，或者将已有Project从一个DC迁移到另一个DC。

• 不能保证最有解，但根据2.1.，只需处理一小部分Project即可

• 需要检测迁移带来的cross-DC带宽，选择成本可控且效果更好的Project进行迁移

3.2. Table Replication (Offline)

将Table的部分partition复制到Job所在的DC，从而节省网络带宽。

对应2.4.的第1点。需要对复制数据占用的额外存储进行trade-off。

3.3. Job Outsourcing (Online)

将Job迁移到另外的DC上，该DC有Job所需的Table数据。

对饮2.4.的第2点。

4. 相关术语与问题定义

4.1. 需要解决的问题

为了控制cross-DC流量，需要解决下面的问题：

• Project Migration问题：

  • 假定有个没有存储限制的DC，我们需要一个启发式方法，在固定存储空闲下，决定一个replica的life span

  • 对于job outsourcing，需要参考静态信息（如迁移后的cross-DC带宽占用，预测的资源利用率）和动态信息（如可用资源等）

• Table Replication问题：需要在存储空间和带宽占用作trade-off

4.2. 定义：Life Span of Table Replicas

• $L_{i}(d)$：对于table $i$，存储在DC $d$上的最近的partition数，即life span

• $S_i$：对于table $i$，复制一个partition到remote DC需要的带宽

  • 上述2个乘积：复制数据到remote DC所需要的存储空间

4.3. 挑战

怎么决定：

• 哪个table的哪些partition需要被复制到哪个DC上

• 找到合适的life span

从而尽可能降低cross-DC访问的带宽，并控制合理的存储大小占用。

5. 分析模型

5.1. 前提假设

• 每个DC之间的单位通信开销一样

• 一个table的每个partition大小一样（按天分区）

• 每天的jobs的访问特征一样

5.2. 模型形式化

首先引入：

1. $R_{i}^{t}(p)$：所有属于project $p$的jobs，从表$i$的分区$p$（在$t$时刻创建）上的读数据量

   等于：$\sum_{j \in J(p)}R_{i}^{t}(j)$

2. $R_{i}^{t}(d)$：所有属于DC $d$的project，从表$i$的分区$p$（在$t$时刻创建）上的读数据量

   等于：$\sum_{p}R_{i}^{t}(p)X_{p,d}$。

   其中$X_{p,d}$：当project $p$在DC $d$里，则值为1；否则为0。

   此外有$R(d)$：DC $d$的table访问矩阵（2维），$R(d)[i,t] = R_i^t(d)$

然后给定一个project placement plan $\mathcal{P}$和table replication plan $\mathcal{R}$，那么对于DC $d$，其所有cross-DC的带宽消耗包括：

• 所有remote read，它不包含在$\mathcal{R}$里

• 复制table的partition到$d$的带宽

即：

1. $BW(d)=\sum_{i:X_{p(i),d}=0}(\sum_{l \ge L_{i}(d)}R_{i}^{t_{cur}-l}(d)+S_{i} \times sgn(L_{i}(d))) $：第一项是复制开销，第二项是remote read开销。

   $sgn(x)$：当$x$大于0时，该值为1，否则为0

而对于DC $d$，所需要的空间大小（包括本地已有和远程复制的）：

1. $S^{rep}(d)=\sum_{i}(S_{i} \times L_{i}(d))$

5.3. 限制

1. 每个project只能属于1个DC

2. 对于每个DC，CPU、内存和存储不能超过其承载能力

3. 此外复制table partition占用的空间也有限制

4. project迁移的数量也有限制

5. 也得考虑有些project不能被迁移

5.4. 目标

需要一个project placement plan $\mathcal{P}$和table replication plan $\mathcal{R}$，在上述假设和限制下，是得所有DC的cross-DC流量最小化，即：$min(\sum_{d}BW(d))$

5.5. 分析

简化：根据第2节，由于大多读的是最近的partition，数据量不大，因此可以认为我们有足够的空间存储table replication的数据，即：

• 5.3.3.的限制可去掉

• 只需决定一个life span，满足其不超过存储上限（5.3.2存储的限制）

6. Solution

6.1. Project Migration

最优的project placement plan，最小的cross-DC带宽占用 $BW^{opt}(d)$ 由下面之一构成：

1. 读取每个表$i$所需的分区数据到DC $d$，如果所需的数据小于该表1个分区的数据

2. 否则，保存表$i$的所有分区于DC $d$，并且每天从其它DC复制最新的分区

因此，$BW^{opt}(d) = \sum_{i:X_{p(i),d}}\min{{\sum_{t}{R_{i}^t(d), S_i}}}$，其中第一项对应1，第二项对应2，取最小值。

目标需达到：$\min{\sum_{d}BW^{opt}(d)}$。

根据2.节所述，只有一小部分表的分区贡献大部分流量，且只需调整一小部分project就能收到很好效果（power-law分布），因此实践上是这样：

1. 根据DC的负载，将project分配到某个DC

2. 设置一个MigCount，只调整一些project，使得$\sum_{d}BW^{opt}(d)$最小化

6.2. Table Replication

6.1.后，我们需要一个table replication plan（即对DC $d$，对于表$i$，找到一个合适的life span $L_{i}$），降低带宽，且保证存储空间限制。

这里认为每天的访问量都是类似的。

这里的$d$被省略，即为某个DC $d$的replcation plan。

6.2.1. DP Solution

定义：

• $dp(i, s)$：对于$i$个表，在$s$存储空间限制下，产生的最小cross-DC带宽开销
  • 对于一个表$i$，其存储开销为$L_{i} \times S_{i}$
• 对于一个表$i$，确定好life span后，其产生的带宽开销为$BW_{L_{i}}$，它为下面2个之和：
  • $\sum_{l \ge L_{i}}{R_{i}^{t_{cur}-l}}$：在life span之外的cross-DC访问带宽
  • $S_{i} \times sgn(L_{i})$：复制的带宽

因此有递推公式：$dp(i,s) = \min_{L_i}{dp(i-1,s-L_{i} \times S_{i})+BW_{L_{i}}}$

但时间复杂度有$O(TLstorage)$，过于昂贵（$T$约$10^6$，$L$约$10^2$，$storage$约$10^9$）。

6.2.2. k-Probe Greedy Heuristic

a. 定义扩展Life Span收益$Gain_{i}^{k}$

使用一个贪心算法，去一步一步的扩展$L_{i}$。

一般而言，扩展$L_{i}$是能降低带宽开销的。因此我们定义一个margin gain，它代表$L_{i}$增加$k$个单位（例如$k$天）能得到的收益（即降低的带宽开销，是一个差值）$Gain^{k}_{i}$：

• 若$L_{i}=0$，margin gain为$(\sum_{0 \le t \lt k}{R^{t_{cur}-L_{i}-t}{i}-S{i}})/(S_i \times k)$

  • 这里要减$S_{i}$，它是复制最新分区的流量

    Q: $S_{i}$是不是要放到$R_{i}^{t_{cur}-L_{i}-t}$的括号里？

• 若$L_{i} \gt 0$，margin gain为$\sum_{0 \le t \lt k}{R^{t_{cur}-L_{i}-t}}/(S_i \times k)$

  • 这里不用减$S_{i}$，因为这部分复制的流量在$L_{i}=0$被cover了

当$Gain_{i}^{k} > 0$时，代表增加$k$个单位life span能节省cross-DC带宽。

b. 算法流程

算法利用最大堆进行贪心，最大堆存储了${Gain_{i}^{k}, i, L_{i}}$，并以$Gain_{i}^{k}$排序。

算法输入：

• $T$：表集合

• $R_{i}^{t}$：表的访问矩阵

• $S_{i}$：一个分区的大小

• $STO^{rep}$：存储budget

• $k$：贪心的k-Probe参数

算法流程：

1. 遍历所有的表，计算所有的$Gain_{i}^{k^{‘}}$（$1 \le k^{‘} \le k$），将其加入到最大堆$maxPQ$里

2. 记录一个$used$，代表复制后使用的存储空间大小

3. 不断弹出堆顶${Gain_{i}^{k^{‘}}, i, L_{i}}$，判断它是否在$STO^{rep}$限制内，若可以，则继续尝试增加$k^{‘}$，计算新的$Gain_{i}^{k^{‘}}$，加入到最大堆$maxPQ$里，并更新$used$

4. 最后$used$会超过$STO^{rep}$，跳出循环，可以记录得到所有表的$L_{i}$

整体时间复杂度：$O(kTL\log{(kTL)})$。远比DP好。

c. 增量更新Replication Plan

上述算法假定访问表的行为特征不改变，生产上还是会改变的。所以replication plan也需要更新。

一种简单的方法就是每隔一段时间（比如$\delta$天）重新跑下上述算法。

这里对$Gain_{i}^{k}$做一些修正：

• $I_{i,t}$：若$tp^{t}_{i}$被replication plan覆盖（被复制了），则值为0，否则为1

• 假设新replication plan cover了 $tp^{t}{i}$ ，那么将6.2.2.b.中的 $R^{t}{i}$ 更新为： $G^{t}{i} = R^{t}{i} - (1-I_{i,t}) \times S_{i}/\delta$ ，然后用 $G^{t}{i}$ 计算 $Gain^{k}{i}$ ，计算公式基本相同

6.3. Online Job Outsourcing

当需要cross-DC访问的数据量非常大的时候，将job迁移到对应DC会有很大好处，但需要考虑：

• remote DC有足够资源

• 将job迁移后，完成的时间（包括等待remote DC）是否小于默认DC

默认下，job会在project所在的default DC创建，使用default DC的quota。

开启job outsourcing后，其它每个DC也会创建对应quota。且我们只迁移一部分的job。

这里定义一个$Score(j,d)$，代表将job $j$迁移到DC $d$的得分，得分越高越倾向于迁移。

$Score(j,d) = \alpha \times \frac{1}{Cost(j,d)} + \beta \times \frac{AvailResrc(d)}{WaitT(j,d)}$：

• $Cost(j,d)$：迁移后的cross-DC带宽占用

• $WaitT(j,d)$：迁移后的job等待时间

• $AvailResrc(d)$：目标DC可用的资源

这里$\alpha$和$\beta$参数需要仔细调优。

7. 系统实现

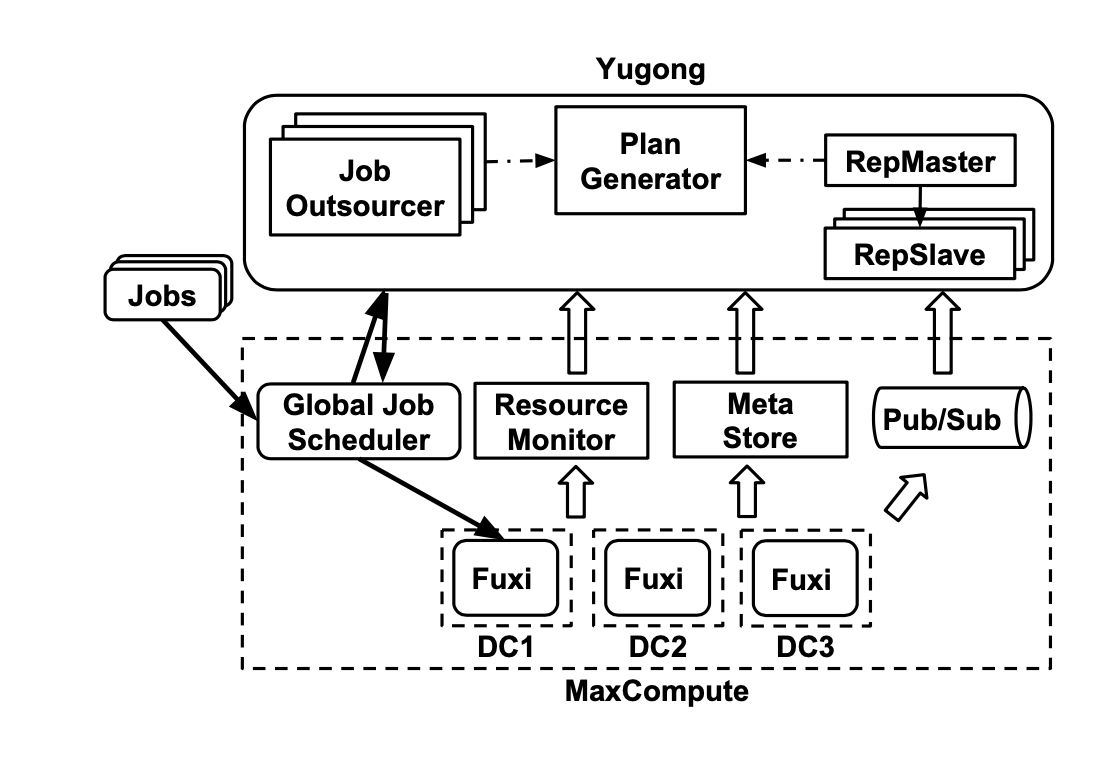
7.1. Plan Generator

用于生成project placement plan和table replication plan。

它：

• 从MetaStore获取cross-DC dependency信息，包括job、table、project的历史统计数据

  • 根据6.1.生成project placement plan

  • 根据6.2.2.生成table replication plan，并且会每隔一段时间更新这个plan

• 从Resource Monitor获取DC的workload和bandwidth使用信息，若有特别大的变动，则会重新生成project placement plan

7.2. Replication Service

用于执行replication plan，服务为master-slave架构：

• master将需要复制表的project均分给下面的slave

• slave执行具体的数据复制任务

  • 从plan generator获取复制的分区信息

  • 向pub/sub订阅，获取project创建表分区的消息

  • 然后启动复制服务（仅对需要的project），向global job scheduler提交复制任务

  • global job scheduer将复制任务分发到对应DC

而复制的流程类似MapReduce的方式，通过多instance并行执行+合并。

触发复制任务需满足3个条件之一：

• 事件触发：当新建了partition，pub/sub会通知，从而触发

• 要求（优先级最高）：当job需要partition的数据，且该partition在replication plan里，但还没有被复制，此时也会被触发

• 扫描：slave会周期扫描replication scan，检查分区是否还需要复制

执行project placement plan：

• 表的分区数据会被复制到目标DC

• job依旧会在原DC创建，直到project迁移完成

• 完成后，删除原DC的table，并更新MetaStore

7.3. Job Outsourcing Service

用于执行job outsourcing，拥有多个实例：

• 从MetaStore和Resource Monitor获取静态和动态信息

• 根据6.3.计算$Score(j,d)$，并决定是否迁移，决策是每个实例独立的

• 向global job scheduler发送必要信息，告诉该job在哪个DC执行

• 此外，还需要把迁移后Job的输出结果返回给原DC（根据2.1.，这部分数据很小）

8. 测试

包含：

• 总体测试：包含cross-DC带宽下降量、replication job的完成时间分布、replication job触发的原因

• Table Replication：

  • 固定的访问模式：k-Probe与理论最优Opt的对比、storage budgets的影响、k大小的影响

  • 动态的访问模式：长时间的测试结果对比、replication plan更新频率的影响、不同更新策略的影响

• Project Migration：包括迁移project数量的影响、以及不同storage budget下k-Probe和Opt的对比

• Job Outsourcing：包括cross-DC带宽下降量，以及不同DC的loading balancing效果

9. 相关工作

• Geo-Distributed Scheduling：如Iridium、Geode、WANalytics、Clarinet、Tetrium、Pixda等工作

• Cloud-Scale Data Warehouse：如BigQuery、Redshift、CosmosDB、MaxCompute

• Caching & Packing：Memcached、Redis etc…

• Cluster Workload Analysis：cluster trace data analysis

10. 总结和思考

充分利用了现实中的2-8定理（例如power-law、zipf的分布），找一小部分突出的问题解决，就能得到接近最优的效果。（近似算法的思想）

这里的k-Probe Greedy就是这样，计算好Gain后，找最突出的几个，在有限步骤里不断更新就行了。

• Previous
  大量CLOSE_WAIT排查
• Next
  C++ 20 Coroutine API Memo & Exploration